Keywords
Collision, Bucket, hash function, key
Hash tables can be used to implement the insert and find operations in constant average time
Its an array with searching of time o(1)
Collision – two keys mapped to same slot
Complexity :
insertions, deletions, and finds in constant average time
Applications :
Implement set in constant time
implement dictionaries, online spelling checkers. If misspelling detection (as opposed to correction) is important, an entire dictionary can be prehashed and words can be checked in constant time. Hash tables are well suited for this purpose because the words do not have to be alphabetized.
Compilers use hash tables to keep track of declared variables in source code. The data structure is called a symbol table.
Hash functions – to map keys into index of buckets in table
Good hash function satisfies uniform hashing – each key equally hash(distributes) to slots
For example, a key that is a character string can be interpreted as an integer expressed in suitable radix notation. Thus, the identifier pt might be interpreted as the pair of decimal integers (112,116), since p = 112 and t = 116 in the ASCII character set; then, expressed as a radix-128 integer, pt becomes (112 128) + 116 = 14452. It is usually straightforward in any given application to devise some such simple method for interpreting each key as a (possibly large) natural number.
(1) Division method :
h(k) = k mod m .
Good values for m are primes not too close to exact powers of 2. For example, suppose we wish to allocate a hash table, with collisions resolved by chaining, to hold roughly n = 2000 character strings, where a character has 8 bits. We don't mind examining an average of 3 elements in an unsuccessful search, so we allocate a hash table of size m = 701. The number 701 is chosen because it is a prime near = 2000/3 but not near any power of 2. Treating each key k as an integer, our hash function would be h(k) = k mod 701
(2) Multiplication method
(3) Universal hashing
Collision by chaining –
Separate chaining hashing is a space efficient alternative to quadratic probing in which an array of linked lists is maintained
• In chaining, we put all the elements that hash to the same slot in a linked list,
• The worst-case behavior of hashing with chaining is terrible: all n keys hash to the same slot, creating a list of length n(like linked list). The worst-case time for searching is thus (n) plus the time to compute the hash function--no better than if we used one linked list for all the elements.
Collisions by open addressing -
• In open addressing, all elements are stored in the hash table itself. That is, each table entry contains either an element of the dynamic set or NIL. When searching for an element, we systematically examine table slots until the desired element is found or it is clear that the element is not in the table. There are no lists and no elements stored outside the table, as there are in chaining
• To perform insertion using open addressing, we successively examine, or probe, the hash table until we find an empty slot in which to put the key.
• Three techniques are commonly used to compute the probe sequences required for open addressing: linear probing, quadratic probing, and double hashing.
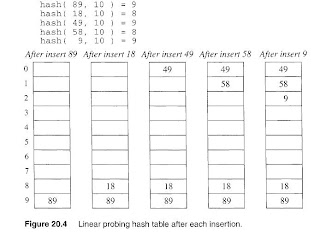
Linear Probing
In linearprobing, collisions are resolved by sequentially scanning table (with wraparound) until an empty cell is found. For example, if there is only one free cell left in the table, we may have to search the entire table to find it
The find algorithm merely follows the same path as the insert algorithm. If it reaches an empty slot, the item we are searching for is not found; otherwise, it finds the match eventually.
Standard deletion cannot be performed because, as with a binary search tree, an item in the hash table not only represents itself, but it also connects other items by serving as a placeholder during collision resolution. Thus, if we removed 89 from the hash table, virtually all the remaining find opera- tions would fail. Consequently, we implement lazy deletion, or marking items as deleted rather than physically removing them from the table. This information is recorded in an extra data member. Each item is either active or deleted.
Quadratic probing examines cells 1,4,9, and so on, away from the original probe point.
if the hash function evaluates to H and a search in cell H is inconclusive, we try cells H + 1 *, H + 22. H + 3*, . . . , H + i2 (employing wraparound) in sequence
Double hashing is one of the best methods available for open addressing
h(k, i) = (h1(k) + ih2(k)) mod m,
Perfect hashing –
• Two level hashing scheme with universal hashing at each level
• First level same as hashing with chaining , instead of making a list of keys hashing to slot J, use a secondary hash table with associated hash function.
Application | Action | Key | Value |
phone book | look up phone number | person's name | phone number |
dictionary | look up word | word | Definition |
Internet DNS | Look up website by IP address | website | IP address |
Reverse DNS | Look up IP address by web site | IP address | Website |
genomics | amino acid dictionary | codon | amino acid |
Java compiler | Find properties of variable | Variable name | Value and type |
stock quote | Look up price of stock | stock symbol | Price |
file share | find song to download | song name | Machine |
file system | find file on hard drive | file name | location on hard drive |
Hash functions – to map keys into index of buckets in table
Good hash function satisfies uniform hashing – each key equally hash(distributes) to slots
For example, a key that is a character string can be interpreted as an integer expressed in suitable radix notation. Thus, the identifier pt might be interpreted as the pair of decimal integers (112,116), since p = 112 and t = 116 in the ASCII character set; then, expressed as a radix-128 integer, pt becomes (112 128) + 116 = 14452. It is usually straightforward in any given application to devise some such simple method for interpreting each key as a (possibly large) natural number.
(1) Division method :
h(k) = k mod m .
Good values for m are primes not too close to exact powers of 2. For example, suppose we wish to allocate a hash table, with collisions resolved by chaining, to hold roughly n = 2000 character strings, where a character has 8 bits. We don't mind examining an average of 3 elements in an unsuccessful search, so we allocate a hash table of size m = 701. The number 701 is chosen because it is a prime near = 2000/3 but not near any power of 2. Treating each key k as an integer, our hash function would be h(k) = k mod 701
(2) Multiplication method
(3) Universal hashing
Collision by chaining –
Separate chaining hashing is a space efficient alternative to quadratic probing in which an array of linked lists is maintained
• In chaining, we put all the elements that hash to the same slot in a linked list,
• The worst-case behavior of hashing with chaining is terrible: all n keys hash to the same slot, creating a list of length n(like linked list). The worst-case time for searching is thus (n) plus the time to compute the hash function--no better than if we used one linked list for all the elements.
Collisions by open addressing -
• In open addressing, all elements are stored in the hash table itself. That is, each table entry contains either an element of the dynamic set or NIL. When searching for an element, we systematically examine table slots until the desired element is found or it is clear that the element is not in the table. There are no lists and no elements stored outside the table, as there are in chaining
• To perform insertion using open addressing, we successively examine, or probe, the hash table until we find an empty slot in which to put the key.
• Three techniques are commonly used to compute the probe sequences required for open addressing: linear probing, quadratic probing, and double hashing.
Linear Probing
In linearprobing, collisions are resolved by sequentially scanning table (with wraparound) until an empty cell is found. For example, if there is only one free cell left in the table, we may have to search the entire table to find it
The find algorithm merely follows the same path as the insert algorithm. If it reaches an empty slot, the item we are searching for is not found; otherwise, it finds the match eventually.
Standard deletion cannot be performed because, as with a binary search tree, an item in the hash table not only represents itself, but it also connects other items by serving as a placeholder during collision resolution. Thus, if we removed 89 from the hash table, virtually all the remaining find opera- tions would fail. Consequently, we implement lazy deletion, or marking items as deleted rather than physically removing them from the table. This information is recorded in an extra data member. Each item is either active or deleted.
Quadratic Probing :
Quadratic probing examines cells 1,4,9, and so on, away from the original probe point.
if the hash function evaluates to H and a search in cell H is inconclusive, we try cells H + 1 *, H + 22. H + 3*, . . . , H + i2 (employing wraparound) in sequence
Double hashing is one of the best methods available for open addressing
h(k, i) = (h1(k) + ih2(k)) mod m,
Perfect hashing –
• Two level hashing scheme with universal hashing at each level
• First level same as hashing with chaining , instead of making a list of keys hashing to slot J, use a secondary hash table with associated hash function.